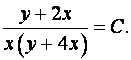Задача 2. Найти общий интеграл дифференциального уравнения.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
2.17. Найти общий интеграл дифференциального уравнения
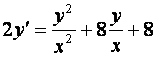
Решение.
Это однородное дифференциальное уравнение. Общий интеграл дифференциального уравнения ищем в виде 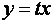 . Тогда
. Тогда 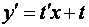 .
.
Дифференциальное уравнение запишется в виде

или

Разделим переменные, умножив уравнение на 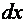 и разделив его на
и разделив его на
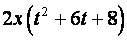 . Получим
. Получим
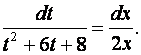
Проинтегрируем полученное дифференциальное уравнение
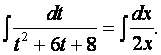
Отсюда
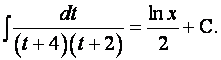
Найдём интеграл
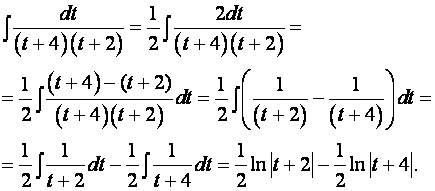
Тогда общий интеграл дифференциального уравнения запишется в виде
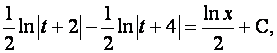
или в виде
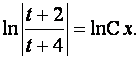
Потенцируем последнее уравнение и учитываем, что
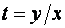 . Получим
. Получим
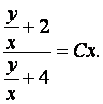
Ответ:Общий интеграл дифференциального уравнения