
|
|
ИНТЕГРАЛ
Первообразная. Неопределённый интеграл. Определённый интеграл
Определение. Функция 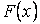 называется первообразной от функции называется первообразной от функции 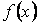 на отрезке на отрезке 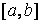 , если во всех точках этого отрезка выполняется равенство , если во всех точках этого отрезка выполняется равенство 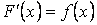 . .
Очевидно, если 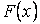 первообразная от функции
первообразная от функции 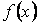 на отрезке на отрезке 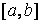 , то для любого постоянного числа , то для любого постоянного числа 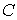 функция функция 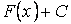 тоже является первообразной для данной функции. тоже является первообразной для данной функции.
Теорема. Если 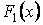 и и 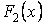 - две первообразные от функции - две первообразные от функции 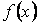 на отрезке на отрезке 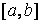 , то их разность равна постоянному числу. , то их разность равна постоянному числу.
Из вышесказанного следует, что если для данной функции 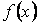 найдена какая-нибудь первообразная найдена какая-нибудь первообразная 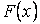 , то любая другая первообразная для
, то любая другая первообразная для 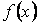 имеет вид имеет вид 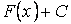 . .
Определение. Если функция 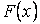 является первообразной для
является первообразной для 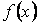 , то выражение , то выражение 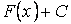 называется неопределённым интегралом от функции называется неопределённым интегралом от функции 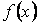 и обозначается символом и обозначается символом 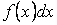 . .
Таким образом,
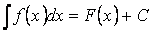
если
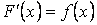
Выражение 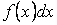 называется подынтегральным выражением, функция называется подынтегральным выражением, функция 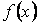 - подынтегральной функцией, а переменная - подынтегральной функцией, а переменная 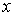 - переменной интегрирования. - переменной интегрирования.
Можно сказать, что неопределённый интеграл представляет собой совокупность всех первообразных данной функции.
Нахождение неопределённого интеграла (первообразной) для данной функции 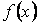 называется интегрированием данной функции. называется интегрированием данной функции.
Определение. Если функция 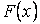 является первообразной для
является первообразной для 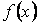 на отрезке на отрезке 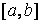 , то число равное разности , то число равное разности 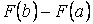 называется определённым интегралом от функции называется определённым интегралом от функции 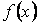 на отрезке на отрезке 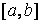 и обозначается и обозначается 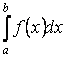
Концы отрезка 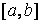 называются, соответственно, нижним и верхним пределом интегрирования. называются, соответственно, нижним и верхним пределом интегрирования.
Таким образом, по определению
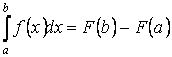
Последняя формула носит название формулы Ньютона-Лейбница. Заметим, что значение определённого интеграла не зависит от выбора первообразной.
Таблица неопределённых интегралов
Свойства неопределённого интеграла
Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если 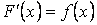 , то , то
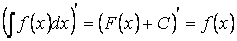
Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
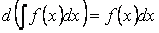
Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы
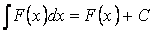
Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов
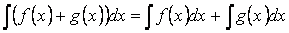
Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов
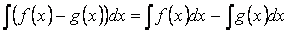
Свойство 6. Постоянный множитель можно выносить за знак интеграла
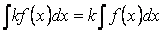
Свойство 7. Если
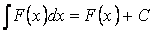
то

Свойства определённого интеграла
Свойство 1. Производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела. То есть

Свойство 2. Определённый интеграл от суммы функций равен сумме неопределённых интегралов
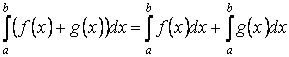
Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла
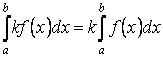
Свойство 4. Если на отрезке 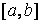 , где , где 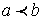 , функции , функции 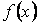 и и 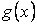 удовлетворяют условию удовлетворяют условию 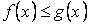 , то , то
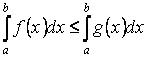
Свойство 5. Если 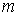 и и  - наименьшее и наибольшее значения функции - наименьшее и наибольшее значения функции 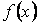 на отрезке на отрезке 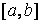 и и 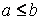 , то , то

Свойство 6. Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак
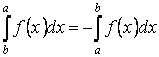
Свойство 7. Для любых трёх чисел 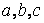 справедливо равенство справедливо равенство
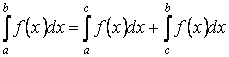
если только все три интеграла существуют.
Свойство 8 (Теорема о среднем). Если функция 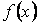 непрерывна на отрезке непрерывна на отрезке 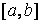 , то на этом отрезке найдётся такая точка , то на этом отрезке найдётся такая точка 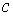 , что справедливо равенство: , что справедливо равенство:
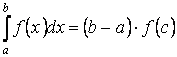
Геометрические приложения определённого интеграла
Если на отрезке 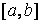 функция функция 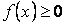 , то площадь криволинейной трапеции, ограниченной кривой , то площадь криволинейной трапеции, ограниченной кривой  , осью , осью  и прямыми и прямыми 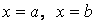 (рис. 9), равна (рис. 9), равна
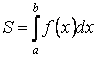
Если  на отрезке на отрезке 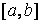 , то площадь соответствующей криволинейной трапеции , то площадь соответствующей криволинейной трапеции
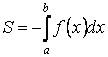
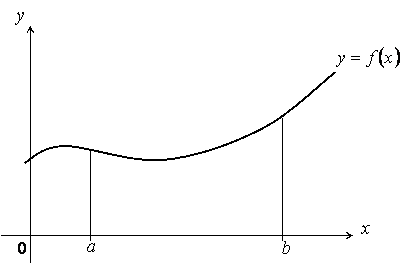
Рисунок 9.
В общем случае, когда функция 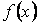 меняет знак на отрезке меняет знак на отрезке 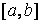 (рис. 10), площадь, ограниченная кривой (рис. 10), площадь, ограниченная кривой  , осью , осью  и прямыми и прямыми 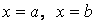 может быть найдена как сумма площадей фигур, лежащих выше и ниже оси может быть найдена как сумма площадей фигур, лежащих выше и ниже оси  . Иначе . Иначе
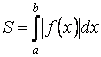
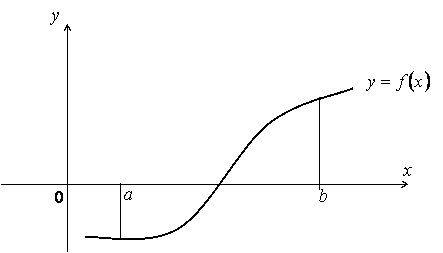
Рисунок 10.
Длина дуги кривой  , ограниченной точками с абсциссами , ограниченной точками с абсциссами 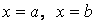 , вычисляется по формуле , вычисляется по формуле
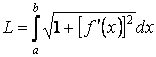
Рассмотрим тело, образованное вращением вокруг оси  криволинейной трапеции, ограниченной кривой криволинейной трапеции, ограниченной кривой  , осью , осью  и прямыми и прямыми 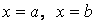 . Объём тела вращения . Объём тела вращения
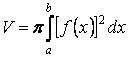
Пусть кривая задана уравнениями в параметрической форме
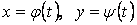 , ,
где  и и 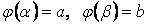 . Площадь криволинейной трапеции в этом случае равна . Площадь криволинейной трапеции в этом случае равна
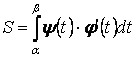
а длина дуги
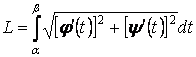
Пусть кривая задана уравнением в полярной системе координат
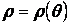 , ,
где 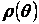 - непрерывная функция, определённая при - непрерывная функция, определённая при 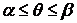 (рис. 11). Площадь сектора, ограниченного заданной кривой и лучами (рис. 11). Площадь сектора, ограниченного заданной кривой и лучами 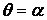 , , 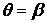 , равна , равна
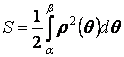

Рисунок 11.
Длина дуги кривой, определённой в полярной системе координат уравнением 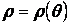 , вычисляется по формуле , вычисляется по формуле

|
|
|

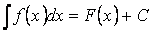
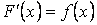
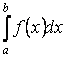
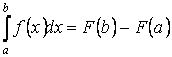
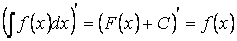
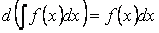
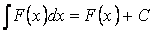
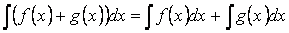
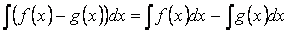
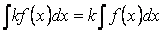
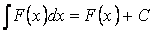


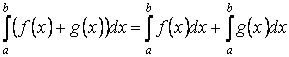
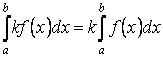
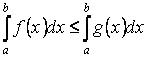

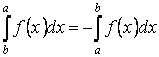
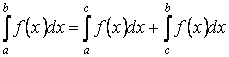
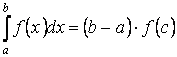
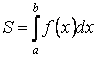
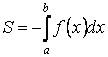

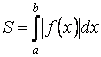

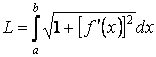
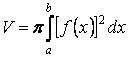
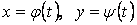 ,
,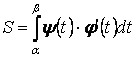
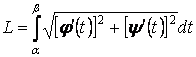
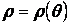 ,
,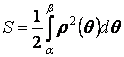


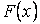 называется первообразной от функции
называется первообразной от функции 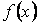 на отрезке
на отрезке 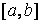 , если во всех точках этого отрезка выполняется равенство
, если во всех точках этого отрезка выполняется равенство 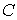 функция
функция 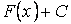 тоже является первообразной для данной функции.
тоже является первообразной для данной функции.
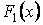 и
и 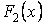 - две первообразные от функции
- две первообразные от функции 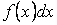 .
.
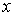 - переменной интегрирования.
- переменной интегрирования.
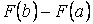 называется определённым интегралом от функции
называется определённым интегралом от функции 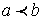 , функции
, функции 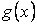 удовлетворяют условию
удовлетворяют условию 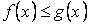 , то
, то
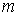 и
и  - наименьшее и наибольшее значения функции
- наименьшее и наибольшее значения функции 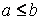 , то
, то
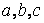 справедливо равенство
справедливо равенство
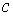 , что справедливо равенство:
, что справедливо равенство:
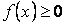 , то площадь криволинейной трапеции, ограниченной кривой
, то площадь криволинейной трапеции, ограниченной кривой  , осью
, осью  и прямыми
и прямыми 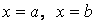 (рис. 9), равна
(рис. 9), равна
 на отрезке
на отрезке  и
и 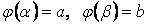 . Площадь криволинейной трапеции в этом случае равна
. Площадь криволинейной трапеции в этом случае равна
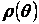 - непрерывная функция, определённая при
- непрерывная функция, определённая при 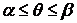 (рис. 11). Площадь сектора, ограниченного заданной кривой и лучами
(рис. 11). Площадь сектора, ограниченного заданной кривой и лучами 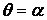 ,
, 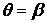 , равна
, равна