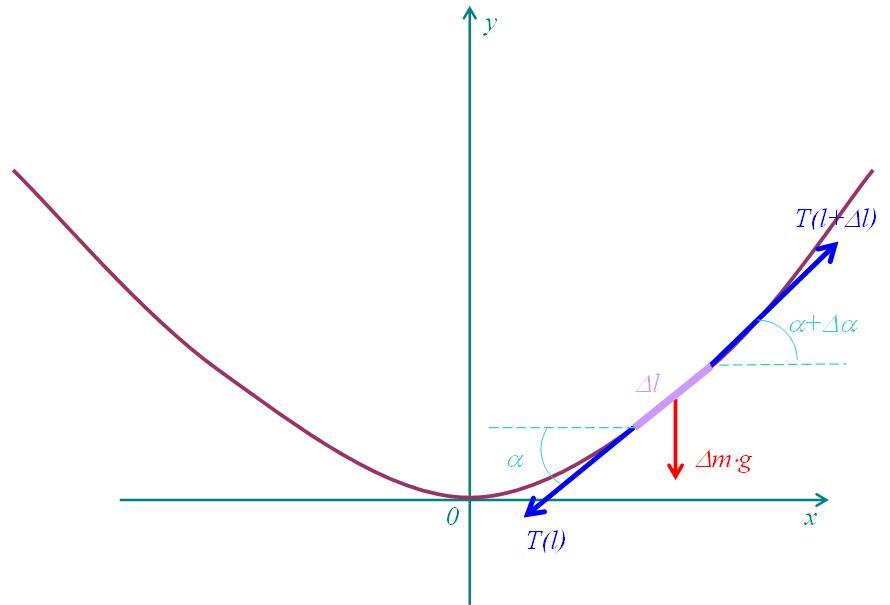
Рисунок 3. Ценная линия и расчётная схема.

        Получили уравнение с разделяющимися переменными, которое после элементарных преобразований принимает вид $$\frac{dz}{\sqrt{1+z^2}} = \frac{\rho gS}{T_0} \cdot dx.$$         Интегрируем последнее уравнение $$\int\frac{dz}{\sqrt{1+z^2}} = \frac{\rho gS}{T_0} \int dx,$$ $$\ln|z + \sqrt{1+z^2}| = \frac{\rho gS}{T_0} \cdot x + C_1.$$         Принимая за начало координат нижнюю точку цепной линии, заметим, что касательная в нижней точке горизонтальная, другими словами, нижняя точка является точкой экстремума для функции \(y(x)\). Следовательно, \(y’(0)=z(0)=0\). Подставим в последнее выражение \(x=0, y=0, z=0\). В результате получим \(С_1 = 0\). Тогда уравнение цепной линии перепишется в виде $$\ln|z + \sqrt{1+z^2}| = \frac{\rho gS}{T_0} \cdot x.$$         Потенцируя полученное уравнение, перепишем его в показательной форме

                            \( z + \sqrt{1+z^2} = exp\left(\frac{\rho gS}{T_0} \cdot x\right) = e^{\kappa x}.\)                           (1)

        Здесь для сокращения записи мы ввели обозначение \(\frac{\rho gS}{T_0} = \kappa.\)
        Умножим обе части уравнение (1) на выражение сопряжённое к левой части \(z-\sqrt{1+z^2}\). Получим $$(z + \sqrt{1+z^2})\cdot(z - \sqrt{1+z^2}) = e^{\kappa x}\cdot(z - \sqrt{1+z^2}).$$         Нетрудно заметить, что $$(z + \sqrt{1+z^2})\cdot(z - \sqrt{1+z^2}) = z^2 - (\sqrt{1+z^2})^2 = z^2 -1 + z^2 = -1.$$         Вследствие последнего замечания, уравнение можно переписать в виде $$e^{\kappa x}\cdot(z - \sqrt{1+z^2}) = -1.$$ или в виде $$z - \sqrt{1+z^2} = -e^{\kappa x}. $$         Прибавим последнее выражением к выражению (1), и поделим полученное равенство на 2. В результате получим $$z = \frac {e^{\kappa x} - e^{-\kappa x}}{2}. $$         Определение 1. Гиперболическим синусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac {e^{x} - e^{-x}}{2}. $$         Определение 2. Гиперболическим косинусом от \(x\) называется функция, определённая следующим выражением $$sh(x) = \frac {e^{x} + e^{-x}}{2}. $$         Предложение 1. Производная от гиперболического косинуса есть гиперболический синус, производная от гиперболического синуса есть гиперболический косинус, то есть$$sh'(x) = ch(x),$$ $$ch'(x) = sh(x).$$         Доказательство. $$sh'(x) = \left(\frac {e^{x} - e^{-x}}{2}\right)' = \frac {(e^{x} - e^{-x})'}{2} = \frac {(e^{x})' - (e^{-x})'}{2} = \frac {(e^{x})' + (e^{-x})'}{2} = ch(x);$$ $$ch'(x) = \left(\frac {e^{x} + e^{-x}}{2}\right)' = \frac {(e^{x} + e^{-x})'}{2} = \frac {(e^{x})' + (e^{-x})'}{2} = \frac {(e^{x})' - (e^{-x})'}{2} = sh(x).$$         Доказательство завершено.     ❑

    Следствие 1. Первообразная от гиперболического косинуса есть гиперболический синус, а первообразная от гиперболического синуса есть гиперболический косинус.

        Следствие 2. $$\int sh(x)dx = ch(x) + C, $$ $$ \int ch(x)dx = sh(x) + C.$$
        С учётом сформулированных определений, а также памятуя о сделанной ранее замене \(z(x)\), перепишем выражение для прогиба в следующем виде $$ y' = z = \frac {e^{\kappa x} - e^{-\kappa x}}{2} = sh(\kappa x).$$
        На основании предложения 1 и следствий к нему, после интегрирования получим $$ y(x) = \int sh(\kappa x)dx = \frac {1}{\kappa} \cdot ch(\kappa x) + C.$$
        В принятой системе координат, когда нижняя точка цепной линии является началом системы координат, справедливо следующее начальное условие \(y(0)=0\). Подставим это условие в найденное уравнение цепной линии и получим $$ y(0) = \frac {ch(0)}{\kappa} + C = 0,$$ $$ \frac {1}{\kappa} \cdot \frac {e^0+e^0}{2} +C = \frac {1}{\kappa} \cdot \frac {1+1}{2} +C = \frac {1}{\kappa} + C = 0. $$ Отсюда \(С=-\frac {1}{\kappa}\) и уравнение цепной линии запишется в виде $$ y(x) = \frac {1}{\kappa} \left(ch(\kappa x) - 1\right).$$
        Таким образом, форма цепной линии определяется как гиперболический косинус с параметром \(\kappa\). Кроме гиперболического синуса и гиперболического косинуса существуют также гиперболический тангенс и котангенс, которые определяются по тому же принципу, что и тригонометрический тангенс и котангенс, а именно:

        Определение 3. Гиперболическим тангенсом от \(x\) называется функция, определённая следующим выражением $$th(x) = \frac {sh(x)}{ch(x)}.$$
        Определение 4. Гиперболическим котангенсом от \(x\) называется функция, определённая как частное гиперболического скосинуса и гиперболического синуса. То есть гиперболический котангенс это функция, определённая следующим выражением $$cth(x) = \frac {ch(x)}{sh(x)}.$$
        Из сделанных определений следуют равенства $$th(x) \cdot cth(x) = 1;$$ $$th(x) =\frac {e^x - e^{-x}}{e^x + e^{-x}};$$ $$cth(x) =\frac {e^x + e^{-x}}{e^x - e^{-x}}.$$
        Исследуем ряд других замечательных свойств гиперболических функций.

        Предложение 2. Справедливы следующие тождества $$сh^2(x) - sh^2(x) = 1;$$ $$1-th^2(x) = \frac {1}{ch^2(x)},$$ $$cth^2(x) - 1 = \frac {1}{sh^2(x)}.$$         Доказательство.

        Из определений гиперболического косинуса и гиперболического синуса следует: $$ch^2(x) - sh^2(x) = \left(\frac {e^{x} + e^{-x}}{2}\right)^2 - \left(\frac {(e^{x} - e^{-x})}{2}\right)^2 = $$ $$ = \frac {(e^{x})^2 + 2e^xe^{-x} + (e^{-x})^2}{4} - \frac {(e^{x})^2 - 2e^xe^{-x} + (e^{-x})^2}{4} = e^xe^{-x} = e^{x-x} = e^0 = 1.$$ Первое тождество доказано. Из него следует $$ch^2(x) = 1 + sh^2(x);$$ $$sh^2(x) = ch^2(x) - 1.$$ Тогда $$1 - th^2(x) = 1 - \frac {sh^2(x)}{ch^2(x)} = \frac {ch^2(x) - sh^2(x)}{ch^2(x)} = \frac {1}{ch^2(x)}.$$ $$cth^2(x) - 1 = \frac {ch^2(x)}{sh^2(x)} - 1 = \frac {ch^2(x) - sh^2(x)}{sh^2(x)} = \frac {1}{sh^2(x)}.$$ Все три тождества доказаны.         ❑


        Задание.
        Найти производные гиперболического тангенса и гиперболического котангенса.

        Решение.
        По правилу дифференцирования частного, получим для производной гиперболического тангенса $$th'(x) = \left(\frac{sh(x)}{ch(x)}\right)' = \frac{sh'(x)\cdot ch(x) - sh(x)\cdot ch'(x)}{ch^2(x)} = $$ $$ = \frac {ch(x) \cdot ch(x) - sh(x) \cdot sh(x)} {ch^2(x)} = \frac {ch^2(x) - sh^2(x)}{ch^2(x)} = \frac {1}{ch^2(x)}.$$
        Аналогично получим производную для функции гиперболический котангенс $$cth'(x) = \left(\frac{ch(x)}{sh(x)}\right)' = \frac{ch'(x)\cdot sh(x) - sh'(x)\cdot ch(x)}{sh^2(x)} = $$ $$ = \frac{sh(x)\cdot sh(x) - ch(x)\cdot ch(x)}{sh^2(x)} = \frac{sh^2(x) - ch^2(x)}{sh^2(x)} = - \frac {1}{sh^2(x)}.$$
        Таким образом, мы доказали следующие соотношения $$ th'(x) = \frac {1}{ch^2(x)};$$ $$ cth'(x) = - \frac {1}{sh^2(x)}.$$
        Обратим внимание на некоторое сходство полученных тождеств с соответствующими тригонометрическими тождествами.